【海軍】談超音速彈丸
2018-02-05 10:20:00
原文网址:https://blog.udn.com/MengyuanWang/110139713
我在前一篇文章討論共軍的新電磁炮時,提到不論初速多高,任何彈丸的海平面平射有效射程都不可能超過40公里。結果自然有人質疑這個結論(不盲目迷信權威,是件好事,即使這個權威就是我),但是因爲這種流體動力學的問題,沒有簡單的理論解,現象極度複雜,我無法在留言欄的有限空間裏好好解釋。考慮了一會兒,覺得雖然有點太專精,但是一般軍迷和媒體都可能會對超音速彈丸受空氣阻力而減速的問題有興趣,卻又從沒有人把它科普過,所以我雖不是彈道學專家,還是以物理人的身份討論一番。不是理工出身的讀者,可以徑行忽略這篇文章。
一般科普文章談到空氣阻力,都說阻力= ρ * A * Cd * v^2 / 2 (v是速度,ρ是空氣密度,A是物體的橫截面),那麽我們只要測量阻力係數Cd,就可以知道在不同速度下,阻力有多大。換句話說,在空氣中穿行的物體,形狀可以很複雜,尺寸大小也各自不同,但是這些影響空氣阻力的種種因素(除了速度、空氣密度和橫截面積之外),全部被包容到一個係數裏去了。例如汽車的Cd,一般轎車在0.28左右,休閑車是0.35,皮卡則接近0.4。這樣的公式,只有在Cd不隨速度變化的前提下才有大用;很巧的是,當速度低於音速時(但不是太接近0),這是一個很好的近似。
然而隨著速度的提高,空氣阻力隨速度的變化,就成爲高度非綫性的。下面的圖是把前面所提的阻力方程式推廣到較大的速度範圍後,畫出Cd隨速度而變的函數。可以看出有四個主要的區域:A)在Mach 0.85以下,Cd基本是一個定值,這是前面提到的,爲什麽會定義Cd這個阻力係數的原因(也是爲什麽民航客機的巡航速度一般都在Mach 0.7-0.85之間);B)從Mach 0.85到Mach 1.1之間,Cd大幅提高,這是因爲音爆激波開始形成,1940年代所謂的“音障”就是研究人員對這個一面墻似的阻力增加所做的描述;C)從Mach 1.1到Mach 5之間,Cd又開始慢慢降低,這段函數其實很接近反比曲綫,換句話説,在這個區間,空氣阻力其實是與速度成簡單正比的(之所以會有這樣的簡單結果,是因爲彈丸的外形不複雜,激波阻力主宰了它們減速的過程),但是科學界因爲約定成俗,仍然繼續使用與速度平方成正比的老公式;D)雖然圖中沒有顯示出來(因爲這張圖裏的兩條曲綫對應著兩種不同的步槍彈,它們的槍口初速只有Mach 3出頭),但是在Mach 5以上,Cd又成為一個定值,一般是在低速數值的一到兩倍之間,視物體本身的形狀和大小而定(物體越粗短,這個比值越高)。
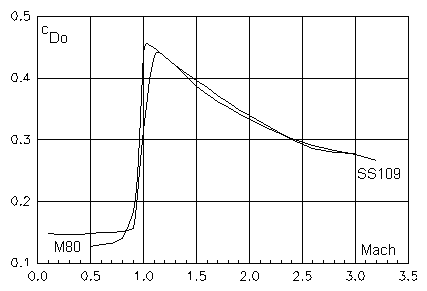
這是一個典型的彈丸阻力係數對速度的函數,縱軸是Cd,橫軸是Mach數。一般會達到超音速的東西,不是彈丸,就是火箭和飛機;火箭和彈丸的函數曲綫比較相似,但是飛機因爲有機翼有攻角(必須產生升力,因此又多了與升力對應的阻力),要更複雜得多,我不在此討論。
軍迷讀者應該常常看到所謂的“亞音速”(或者“次音速”,“Subsonic”)、“穿音速”(“Transonic”)、“超音速”(“Supersonic")和“高超音速”(“Hypersonic”)等詞匯,它們的定義來源正是上面所描述的空氣阻力係數作爲速度的函數曲綫,有不同形狀的A、B、C和D四個區間。
好,我們對空氣阻力和速度的關係有了基本的瞭解,現在可以回頭來討論本文的主題,也就是電磁炮的彈丸在海平面空氣中的減速現象。目前實用電磁炮可能達到的初速,頂多是Mach 7,更可能是Mach 5,所以主要是在前面所提的C(超音速)區間。如前所述,在這個區間,空氣阻力其實是與速度成簡單正比的。學過大一微積分的讀者,可以試著從這個正比關係來推導彈丸減速的規律,你們應該會發現,彈丸速度會隨距離而做綫性損失;但是損失的斜度視彈丸的形狀而定,必須從實驗求得。
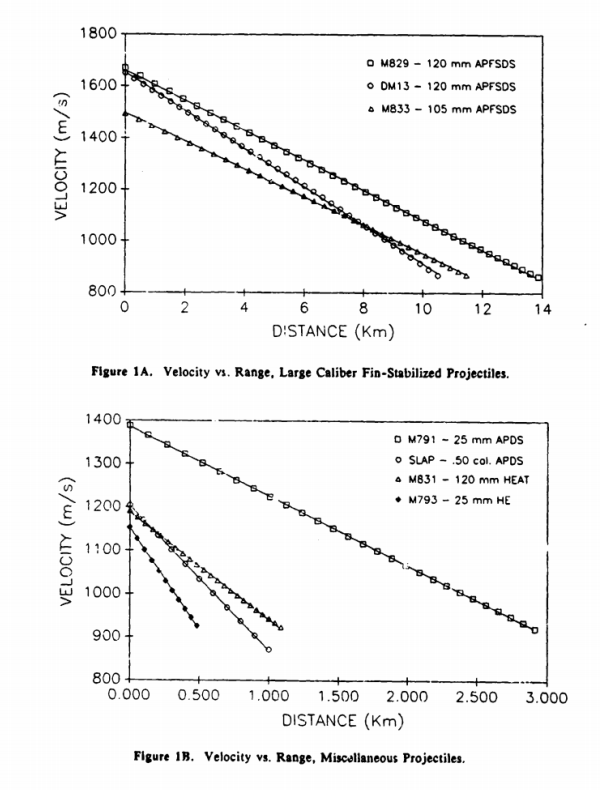
這兩張圖來自1990年美國陸軍彈道實驗室(US Army Ballistic Research Laboratory)的一篇論文(參見http://www.dtic.mil/dtic/tr/fulltext/u2/a224217.pdf ,已經解密了)。圖1A是三種APFSDS(翼穩脫殼穿甲彈,亦即阻力極小的次口徑長杆飛行物)的速度對距離函數,圖1B則對應著幾種小口徑彈丸。它們都高度符合綫性關係,可見在超音速區間空氣阻力與速度成簡單正比是一個很好的近似。
這裏我們先看看圖1A的最上方曲綫和圖1B的最下方曲綫,分別對應著極爲細長的M829(即M1坦克所用的120毫米穿甲彈)和比較粗短的M793(是典型的小口徑高爆彈丸)。我的估計是前者的斜率是-0.13(單位是Mach/km,亦即每公里損失的Mach數),後者的斜率則是-1.3,剛好高了10倍。人類可以做出來的海軍艦炮彈丸,只要重量在30千克以下,不論是火炮還是電磁炮,在海平面Mach 1.1到Mach 5之間的速度損失率,基本都應該在這兩個數值之間。以下的討論將取速度衰減係數k = 0.13來代表大型次口徑長杆動能彈,用k = 0.3來代表典型的大口徑高爆彈。
現有的典型海軍艦炮,例如美軍的Mark 45五寸炮,發射高爆彈的初速是Mach 2.3(如果要改用APFSDS,因爲彈丸較輕,初速應該更高,可能可以接近Mach 3;120毫米和125毫米的陸軍坦克炮,發射APFSDS都可以達到Mach 5),有效射程號稱是24公里,但是這其實早已是曲射了,速度也掉到音速之下。荷蘭的Goalkeeper近防炮發射次口徑脫殼彈的初速是Mach 3.3,有效射程2公里。上圖中最接近它形狀和大小的,是M791(1B裏的最上方綫),對應著大約k = 0.5,所以我們可以估計終端速度是3.3 - 0.5 * 2 ≈ Mach 2.3,這才是平射彈應有的最低水平。陸軍的坦克炮也是同樣的道理,M829的初速是Mach 4.9,k值是前述的0.13,在4公里的有效射程外,終端速度還有Mach 4.4,陸軍卻不吹噓更高的射程了。
如果電磁炮發射APFSDS,那麽40公里外的Mach數損失是0.13*40=5.2,即使初速是Mach 7(請注意,Mach 5以上這個公式其實已經不適用,實際的阻力與速度平方成正比,比速度正比更高得多,所以Mach數損失應該高於5.2,更精確的估算是5.5左右,方法參見下一個段落),終端速度也只在Mach 1.8以下(實際上是Mach 1.5),還不如雄風三型飛彈,但是卻沒有任何高爆藥,所以其破壞力也就只是一個小洞(讀者請想想雄三的純動能損害還不足以擊毀一艘小漁船,何況炮彈比飛彈更小了一百倍左右)。如果這個電磁炮平射高爆彈,那麽17公里外的Mach數損失就已經超過0.3*17=5.1,Mach 7的初速更是完全沒有意義。
同樣用大一微積分,可以簡單求得在Mach 5以上,因爲阻力是與速度平方成正比,速度對距離會成指數下降,亦即v ∝ e^(-x/D)。考慮APFSDS做爲最低阻力的例子,可以求得D=5/0.13 ≈ 40公里(嘿嘿,你們以爲40公里是我隨口亂説的嗎?);換句話説,在Mach 5以上,每40公里,速度降低為原本的37%(這是Euler常數e的倒數)。所以如果在40公里外,要求終端速度為Mach 5,那麽初速必須是5 * e ≈ Mach 14。別説這是21世紀身管材料科技不可能達到的高度,就算外星人送給我們新的超級耐磨耐熱材料,能做出Mach 14的電磁炮,空氣阻力所造成的摩擦生熱也達到Mach 5的八倍,足以融化鎢芯彈丸。
【後註一】因爲在留言欄談起來,我順便提一提。要算曲射的射程比較麻煩,首先必須知道大氣密度對高度的函數,請參見下圖:
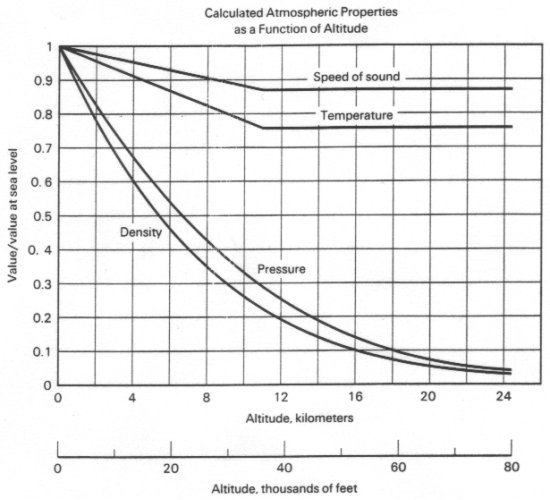
這個函數曲綫很類似一個指數,我取ρ ∝ e^(-z/H),這裏H可以從圖上直接讀出,大約是7.7公里;換句話説,每上升7.7公里,大氣密度減低為原本的37%。然後也不須要寫程式來解那套微分方程組,Excel這種電子表格已經綽綽有餘。我放了幾個傳統火炮發射大口徑(120-130毫米)高爆彈的初速、射高和射程數據,反推到的速度衰減係數k都是0.3,這就是本文稍早選擇k = 0.3來代表大口徑高爆彈的理論基礎。
至於美軍那門Mach 5初速(對應著炮口動能=32MJ,這是因爲他們用的彈丸重22千克,剛好和120、122、125毫米口徑的高爆彈類似,所以前面我選用120-130毫米口徑的火炮彈丸來估算出k = 0.3,是有道理的)的電磁炮,如果不用火箭助推和滑翔增程,最大的自由彈道射程是多少呢?我的計算結果是55公里,對應著58°的發射仰角;這剛好是廠商吹噓的最大射程220公里(120海里)的1/4,只比初速大約Mach 2.7的既有155火炮發射Base Bleed彈丸(底排彈雖然看來有火焰,其實不是火箭助推,所用的火藥很少;BB的用處,是吹走彈丸後方的低壓區,以避免Karman Vortex Street,也就是造成旗幟在風中飄揚的那個渦流作用;我以後會寫專文介紹)多出13公里,可見靠增加初速來提高射程,是件事倍功半的傻事(海軍實在應該先問問陸軍,明明已經有Mach 5的平射坦克炮,爲什麽不把同樣的技術應用在曲射榴彈炮上)。換句話說,電磁炮連用在遠程曲射對地轟擊,都不見得是效費比最高的方案。
【後註二】留言欄裏,有讀者提起一戰時代的巴黎炮,初速接近Mach 5,彈丸重152千克,有120公里以上的射程(歷史記錄不太確定)。我的回答已經暗示了(但沒有明説,所以在這裏講清楚),22千克的彈丸初速到達Mach 5之後,要增加自由射程,額外的動能其實最好是用來增大彈丸而不是提高初速,因爲前者可以減低速度衰減係數k,而後者卻會提高k(即從綫性減速變成指數衰減)。那麽電磁炮的設計者爲什麽反物理定律而行呢?這其實是商業考慮:電磁炮轉化能量的效率比火炮低很多,所以總動能有嚴格的上限,但是火炮要達到Mach 5並不難,電磁炮能量小、射速低、設備昂貴龐大複雜,基本一無是處,唯一的賣點在於有可能達到Mach 7,所以賣家的忽悠只好圍繞著這個唯一的特點來做文章,那麽彈丸就只能拼命輕量化,不能超過22千克。
目前電磁炮的原型機只達到32MJ的炮口動能,在可見的未來,不會超過64MJ,我們可以拿這些數據來和歷史上的幾個著名火炮做對比:
1)巴黎炮:彈重152千克,初速Mach 4.9,動能220MJ;
2)大和號的18寸炮:穿甲彈重1460千克,初速Mach 2.3,動能440MJ;
3)Gustav 800毫米炮:穿甲彈重7100千克,初速Mach 2.0,動能1840MJ。
當然,後兩者不是為射程而優化的,但是它們卻用二戰時代的技術達到了電磁炮完全不能企及的動能水平,又一次地曝露了電磁炮相對於火炮技術的局限性。至於火炮針對射程優化之後,能達到什麽程度?Bull博士在被以色列暗殺之前,用1980年代的技術為伊拉克設計了兩型火炮,叫做Project Babylon,其中第一代的小號炮叫做Baby Babylon,口徑350毫米,自由彈道射程750公里,我的Excel電子表格說初速必須在Mach 9以上,假設是Mach 9,彈重700千克,那麽炮口動能是3300MJ,比電磁炮的極限高出50倍。
22 条留言
巨大的列车都能悬浮起来,相对小的电磁炮弹解决起来也不是难事,军舰要比列车的空间还要大,容纳高温超导磁悬浮设备的空间更大。
假如电磁炮弹悬浮在电磁炮的炮座上,发射时就不会对“炮管”造成摩擦,这个问题也就不是问题了。//
http://www.hongdezk.com/a/hantangguilai/20180204/195168.html
以上是刀口的意見(僅指悬浮炮管方面), 供大家參考.
另外一个评论的朋友,电磁轨道炮EMRG正常工作需要和导轨非常良好的接触,接触点需要通过几千安培以上的电流。磁悬浮技术只可能应用于其他类型的武器。
電磁炮和Zumwalt的155炮要用曲射分別打到360和180公里,也是大忽悠。考慮不同高度時的大氣密度,你可以用我這篇文章裏的公式,來發現根本不可能有那樣的彈道射程。美國軍工廠商宣稱的射程數據,都是利用火箭助推再加上滑翔增程,而且火箭占了全彈的一大半,彈頭基本沒有威力。如果是純粹的自由飛行彈道,射程連1/3都沒有。
有勞王兄指正.
哇哈哈, 其實.......這已經是刀口通篇文章裏, 最靠譜的一個論點了, 其餘的, 唉.
若真如此,也是好事,说明战忽局的工作受重视了,要提升软/巧实力,下一步希望轮到媒體和对外研究吧。
如果想要更高的发射速度,那不好意思,就要求助于本文的主角——电磁炮!//
https://mp.weixin.qq.com/s/LxZVU0Z2NKeJIIzqfBhCWQ
唉,还有更「精彩」的。这篇所謂科普,图文並茂,正合文科生的口味。最妙的是,它还无意间「呼应」了王兄以下一段幽默:
(嘿嘿,你們以爲40公里是我隨口亂説的嗎?)
哇哈哈哈哈哈哈哈哈哈!
可惜電磁炮不但在戰術實用上不靠譜,在忽悠美國這個目的上也希望渺茫。這是因爲美國人已經投入了十幾年的資源,原型機的工程化已被嘗試過了,所以我提的電磁炮毛病和缺點他們清楚得很,中方的宣傳很可能只會讓他們暗笑在心。
再想請教王博士,大陸獨步全球的激波風洞技術是否有可能微型化後提供電磁砲管內減少阻力或摩擦力甚至提供部分推力的幫助呢?
从这张图看,电磁炮的射程还是很可观的,当然中短期内不实用是真的。
http://digitalpaper.stdaily.com/ ... t_368149.htm?div=-1
如此强大的单舰平台,马伟明称之为“全能舰”,对其攻防性能逐一进行了设想。防空分为3个层次:200—600公里范围,使用可重复自动装填的通用电磁发射装置发射反导导弹,实现点对点防御;10—200公里,利用电磁轨道炮实现目标面拦截;10公里以内,利用激光炮作为最后一道防线,对末端导弹进行拦截。反潜和反鱼雷上,利用电磁发射装置发射反潜导弹对潜艇进行攻击,利用电磁线圈炮对来袭鱼雷进行拦截。 在反舰与对陆攻击体系的构想中,“全能舰”将形成3层火力圈:600—1000公里,使用可重复自动装填的通用电磁发射装置发射远程巡航导弹和弹道导弹,完成对海和对岸目标攻击;200—600公里,利用电磁火箭弹(炮),进行对海和对岸目标攻击;200公里以内,利用电磁轨道炮完成对海和对岸目标的攻击,一具电磁轨道炮可将对岸打击能力提高一个数量级。
按照马伟明的“全能舰”计划来看,海军是打算把电磁“炮”当作未来可能的战争模式改变者之一。
另外,陆军应该也是准备要上“电磁迫击炮”和第四代全电坦克的“电炮”。
我个人倒是不把电磁炮当作“炮”来看待,与其说是“炮”,不如说是“质量投送器”,长远来看,还是大有可为的。
我寫了三篇文章,洋洋灑灑,在這裏最後那一段還做了很淺白的總結,核心論點就是你給的這些圖片和宣傳,都是謊言,結果你還是來照本宣科一番。
32MJ就是Mach 5初速(64MJ就是Mach 7初速)的電磁炮,他們說可以打到120海里,也就是220公里,但是我的論證發現實際上只有1/4,也就是55公里的射程,其餘的165公里,是用火箭助推和滑翔增程搞出來的,代價就是1)整個彈頭的質量和空間都被用到火箭、滑翔翼和引導頭上了,根本沒地方放高爆藥,2)因爲要讓引導頭和滑翔翼能承受極大的加速g力,比同射程的導彈和火箭彈還貴好幾倍。
做白日夢很容易,但是憑空胡扯些數據被打臉之後,至少要有尊重邏輯的態度。600-1000公里的射程的導彈,需要用電磁彈射來增加不到10公里(我的論證發現Mach 5初速只增加13公里的實際射程,大型導彈不可能以電磁彈射加速到Mach 5)的射程嗎?如果價錢是0,或許可以的,但是絕對沒有實戰上的大影響(實際上發射射速比起垂直發射大爲減低,不適合用在必須對抗飽和攻擊的對空導彈)。
射程是300公里的火箭彈,有必要換成貴100倍而且彈頭載荷小10倍,“射程”只有220公里的電磁炮嗎?絕對沒有。謊言重複1000000遍,還是謊言,只不過成了1000000個蠢蛋相信的謊言。
我認為這個可能不能排除, 但也不是說一定有這個可能, 總之令人懷疑.
網路上一直有人攻擊中共用五毛控制輿論,
我可以肯定的說,
長久以來美日台獨就已經用類似雇用五毛的手法控制引導或將某些別有居心的看法加入輿論.
就算這個" 临高启明"不是敵人,
還是有很多人, 可一概稱之為敵人, 不希望我們知道真相, 包括電磁炮的真相.
不過我一直懷疑電磁炮原本就是美國人的忽悠。
与此同时,昨天中国又在境内进行中段反导试验,这对美帝核武政策调整具体的回应点在哪呢?距离上一篇讲反导试验的文章过去快4年了,不知道这几年间老共技术精进几何?
跟高彈道狀況,要飛的遠,就把彈丸打到平流層之上,
等彈丸落下時的終端速度也很可觀了!
至於流體力學,我只是個好奇的業餘人士,你也知道它實際上有多麽複雜和困難。正是因爲如此,我從來沒有找到簡單易讀的科普。這次我能寫出一篇精確的半專業討論,對一個重要話題提出解答,而且還是一般理工科的讀者都應該能看出頭緒的文章,是個我很自豪的創舉。
王孟源博士您寫這一份科普文章,內容對想知道火炮外彈道特性的理工人而言,有相當的幫助,只不過临高启明先生對超高初速火炮曲射射程的相關計算,也是有所本的,證據在哪呢?因為對於炮口初速達到接近馬赫5 (1701 m/s)的火炮系統,人類在100年前已經造了出來,也就是1918年三月21日投入實戰的巴黎炮。其初速根據戰後考據資料為馬赫4.82 (1640 m/s),實戰中達到的最大射程約為120 km,而且炮彈並非長桿低阻力型式而為高爆彈體,其相關計算可見
http://www.vcsp.info/Chapter_8/Application_to_Long-Range_Artillery_-_Shelling_Paris_in_WW1/Shell_Trajectory_in_Atmosphere_on_a_Rotating_Earth.aspx
不過此一計算似乎把炮彈的阻力係數設到只有0.18,可能跟王博士您的設定k=0.3低了不少,基於對於事實和邏輯的追求,在這裡想找一下還有哪一個環節的計算可以讓最後的結果有所差異。
這裏的真正重點是爲什麽巴黎炮的速度衰減係數只有0.17。巴黎炮原本口徑是211毫米,彈丸質量是106千克。後來口徑擴增到238毫米,對應的彈丸質量沒有資料,但是我們可以很簡單地等比例放大,求得估計值為152千克。這樣的彈丸比我討論的120+毫米高爆彈大7倍。速度衰減係數隨尺寸增加而減低,所以從0.3降到0.17很正常。我在前一篇文章也暗示過,要用Mach 5把彈丸送出100+公里,做到8寸就行了。若是能做到16寸,那麽説不定k會降到0.13(這必須靠實驗才能確定),我的Excel說射程會是160公里。
但是電磁炮能隨意增加彈丸質量嗎?22千克Mach 5的彈丸,動能是32MJ;152千克Mach 5的彈丸,動能卻是220MJ。美國人連做夢都只敢做到64MJ。而且152千克的巴黎炮彈,裝藥只有6千克,和41千克的155炮彈一樣,你覺得這划算嗎?
對於我們航太相關系所畢業的人,會覺的很怪,火箭增程砲彈,也是很成熟的東西,對於傳統砲彈,至少增加30-40%的射程!
火箭增程30-40%,的確是很普通的技術了,但是美國電磁炮的廠商要增程300%,這其中的貓膩很是可觀。
軌道炮和電磁彈射器,在電力供應系統上有共通,但是實際發射機制是不一樣的。
中国首创电磁火箭技术,弹射到空中点火,技术领先猎鹰9_搜狐军事_搜狐网: http://t.cn/RRwEiar
(xpure@foxmail.com)
大型火箭是很脆弱的東西,要加固到能用電磁彈射,增加的死重得不償失。
電磁炮很可能還是會被用在055A或055B上,但是背後的考量很複雜,我正在寫另一篇文章。
看过一篇科普文,说高尔夫球并不是光滑的,而是四周坑坑洼洼。这种设计考虑了空气动力学,可以使球的飞行距离比光滑的球长一倍。我的问题是,炮弹是不是也可以考虑这种坑坑洼洼的设计?使飞行距离变长?
谢谢您
博主我想做个ODE的RK4数值积分看看到底能飞多远,假设M5, M32J,22kg, 考虑密度高度变化 Cd按你图里SS109取,炮弹面积怎么取?125mm直径?
122毫米的高爆彈重量剛好很接近22千克。